FE Exam Review – Transportation Engineering – Traffic Stream Parameters

Traffic streams are characterized by a number of different operational
performance measures. Traffic operating free from traffic control devices, intersections, signs, etc, is characterized as uninterrupted traffic flow.

The following traffic stream parameters can help us characterize his uninterrupted traffic flow and ultimately arrive at performance measures.

Traffic flow, speed, and density are variables that form the foundation of traffic
analysis. Every transportation engineer should understand the basics behind each variable and how they all interconnect.

Note: We will use the NCEES FE Handbook 10.1 denotation for flow, speed, and density. 

Flow = V
Speed = S
Density = D 

Flow (\(V\)) or volume

Flow volume or flowrate is the number of vehicles (n) passing a point on a road or a lane during a specified time period.

\begin{equation}
V=\frac{n}{t}
\end{equation}

Where, 

\(V=\) traffic flow in vehicles per unit time

\(n=\) number of vehicles passing some designated roadway point during time \(t\)

\(t=\) duration of time interval

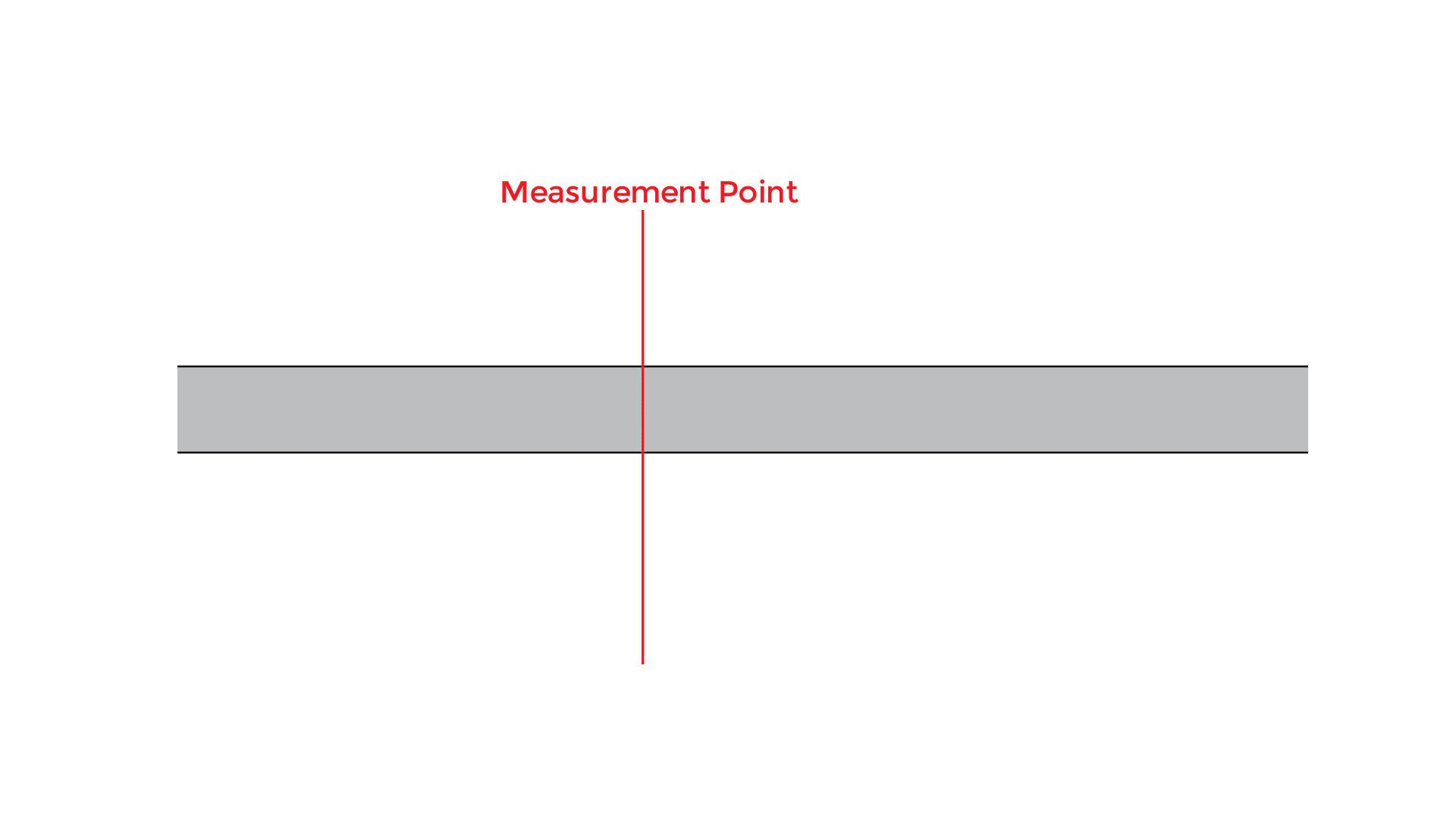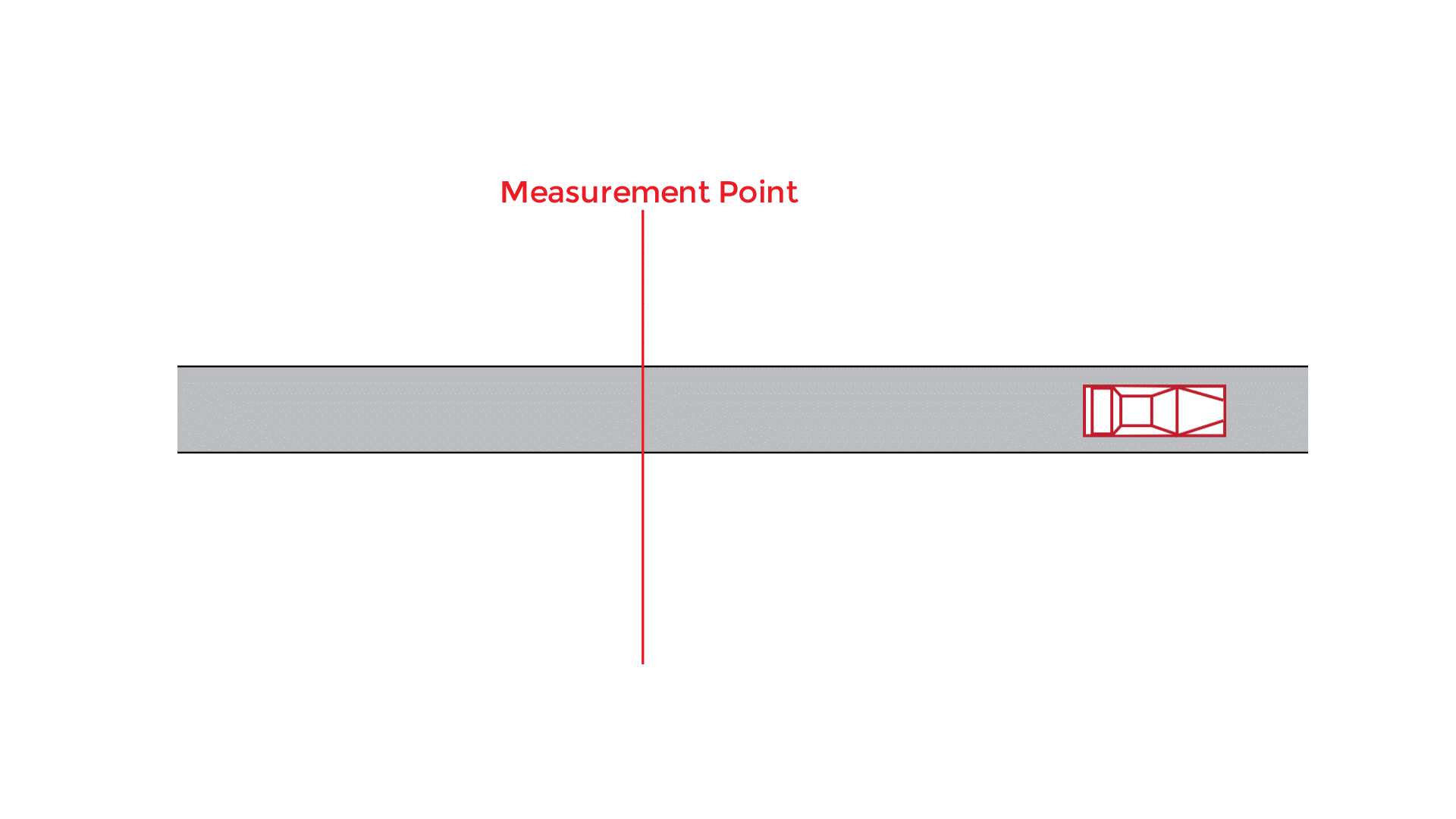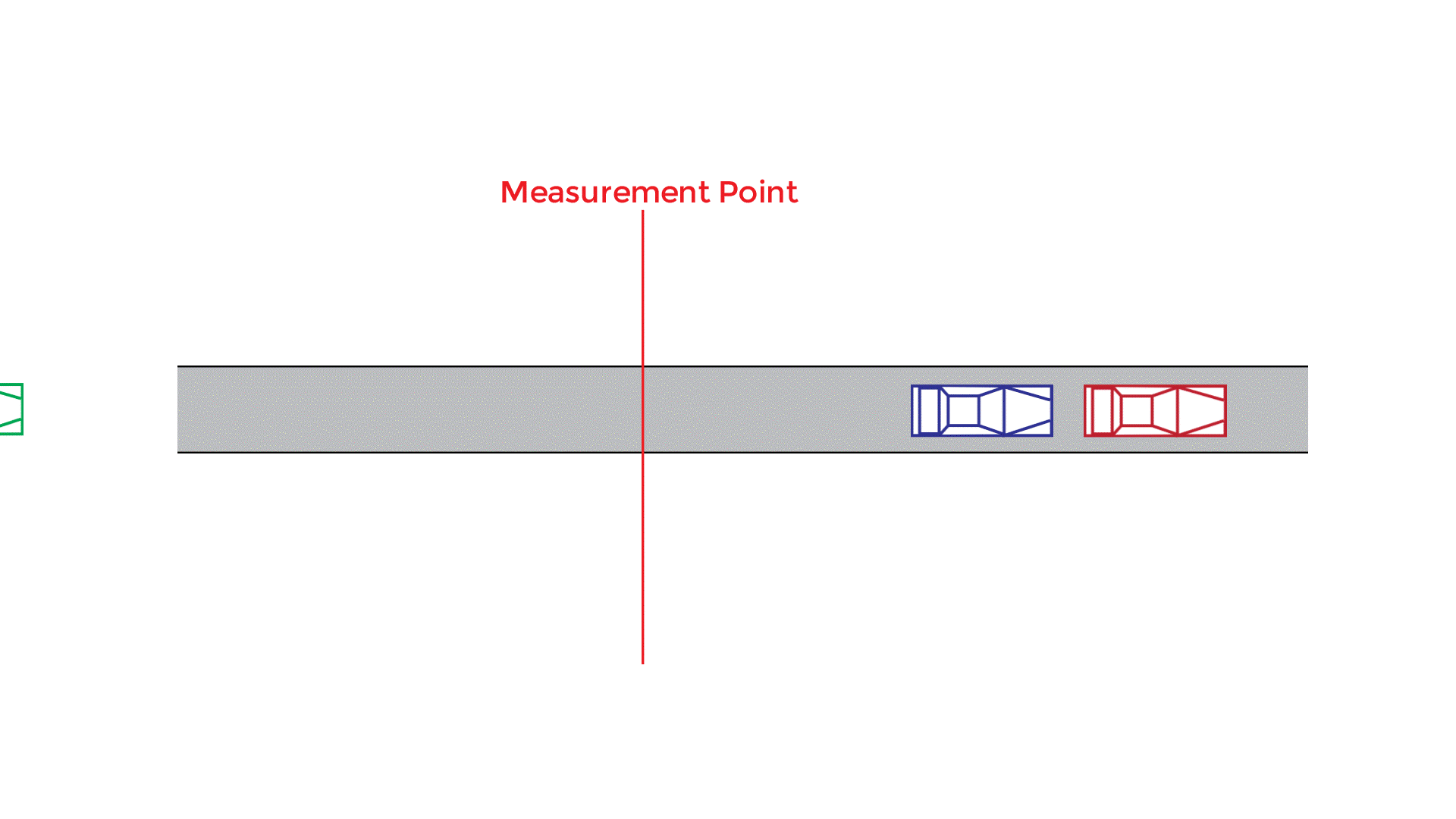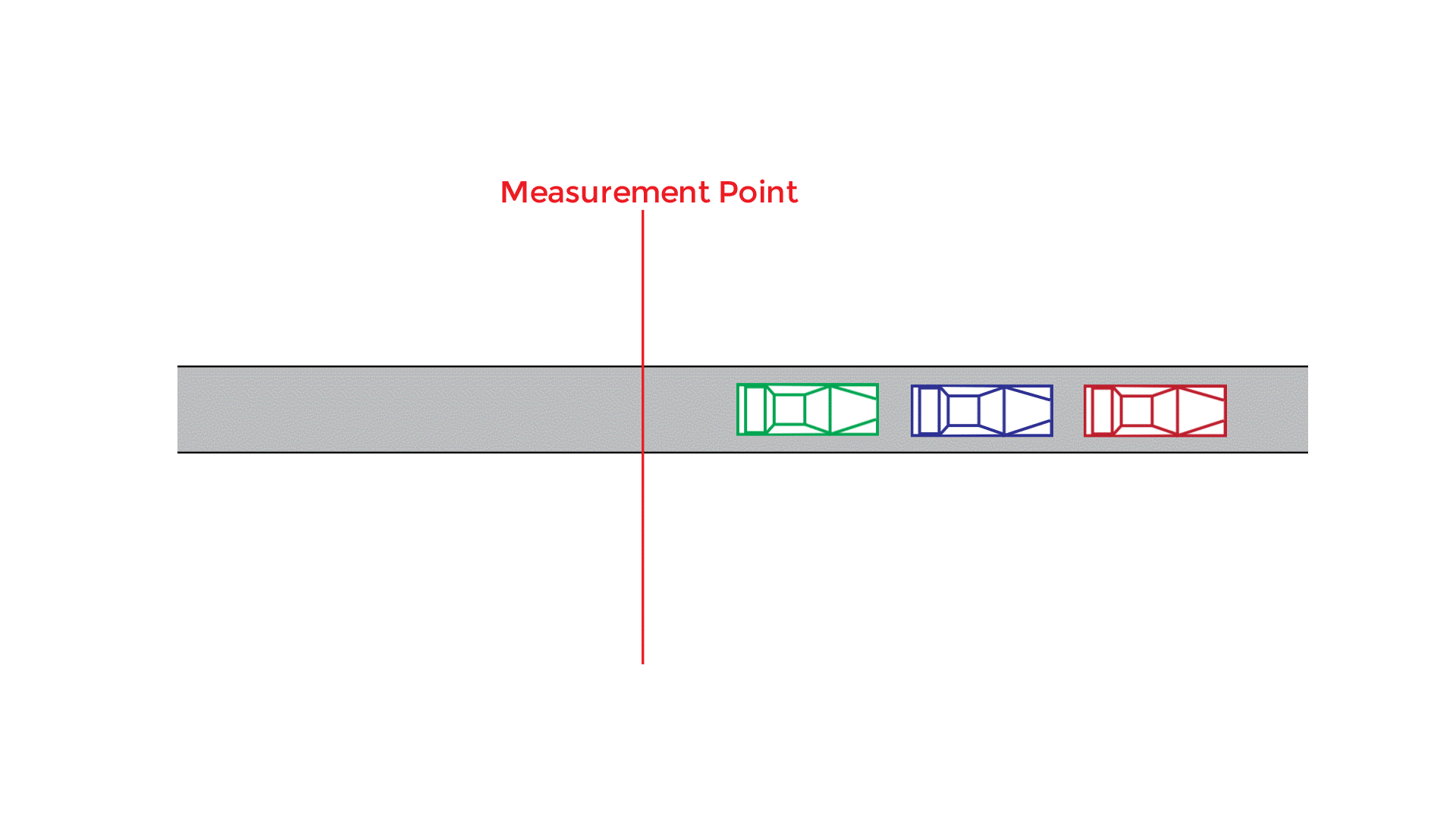
The flowrate is related to the space mean speed (SMS) and density (D) by the following equation:

\begin{equation}
V=S M S \times D V=S \times D
\end{equation}

The units for flowrate is typically given as vehicles per hour (veh/hr).

Density (\(D\)) 

The density is the number of vehicles (n) occupying a given length of a lane or a roadway at a particular instant expressed as vehicles per mile (veh/mi). The density is a measure directly related to the traffic demand and it is the most important parameter used to measure the quality of traffic operation.

\begin{equation}
D=\frac{n}{L}
\end{equation}

The density can also be related to the individual spacing between successive vehicles (measured from front bumper to front bumper). The roadway length, \(L\), is defined as: 

\begin{equation}
L=\sum_{i=1}^{n} s_{i}
\end{equation}

Where, 

\(s_{i}=\) spacing of the \(i\) th vehicle (the distance between vehicles \(i\) and \(i-1\), measured from front bumper to front bumper)

\(n=\) number of measured vehicle spacings

The units for density is typically given as vehicles per mile per lane (veh/mi/lane).

Speed (\(S\)) 

The speed is the distance traversed by a vehicle in unit time, expressed in terms of miles per hour (mph).

• • In a traffic stream, the speed of different vehicles need not be the same at a given time and location.
  • Therefore the speed of a traffic stream is not a single value, but is a distribution of individual vehicle speeds – time mean speed and space mean speed.

\begin{equation}
\text { Average Speed }(S)=\frac{\text { Flowrate }}{\text { Density }}=\frac{V}{D}
\end{equation}

1) Time Mean Speed (TMS) – the average speed of vehicles measured at a point or location over a given time interval – this is also called spot speed. Often used for spot speed studies. 

2) Space Mean Speed (SMS) – the average speed of vehicles measured at an instant of time over a specified stretch of road (distance d involved). Often used for travel time studies and this is the speed variable used in traffic models.

Note: The Space mean speed is always less than the time mean speed. 

3) Free Flow Speed (FFS) – the optimal vehicle speed in which “no congestion conditions” or very low volume conditions are present.

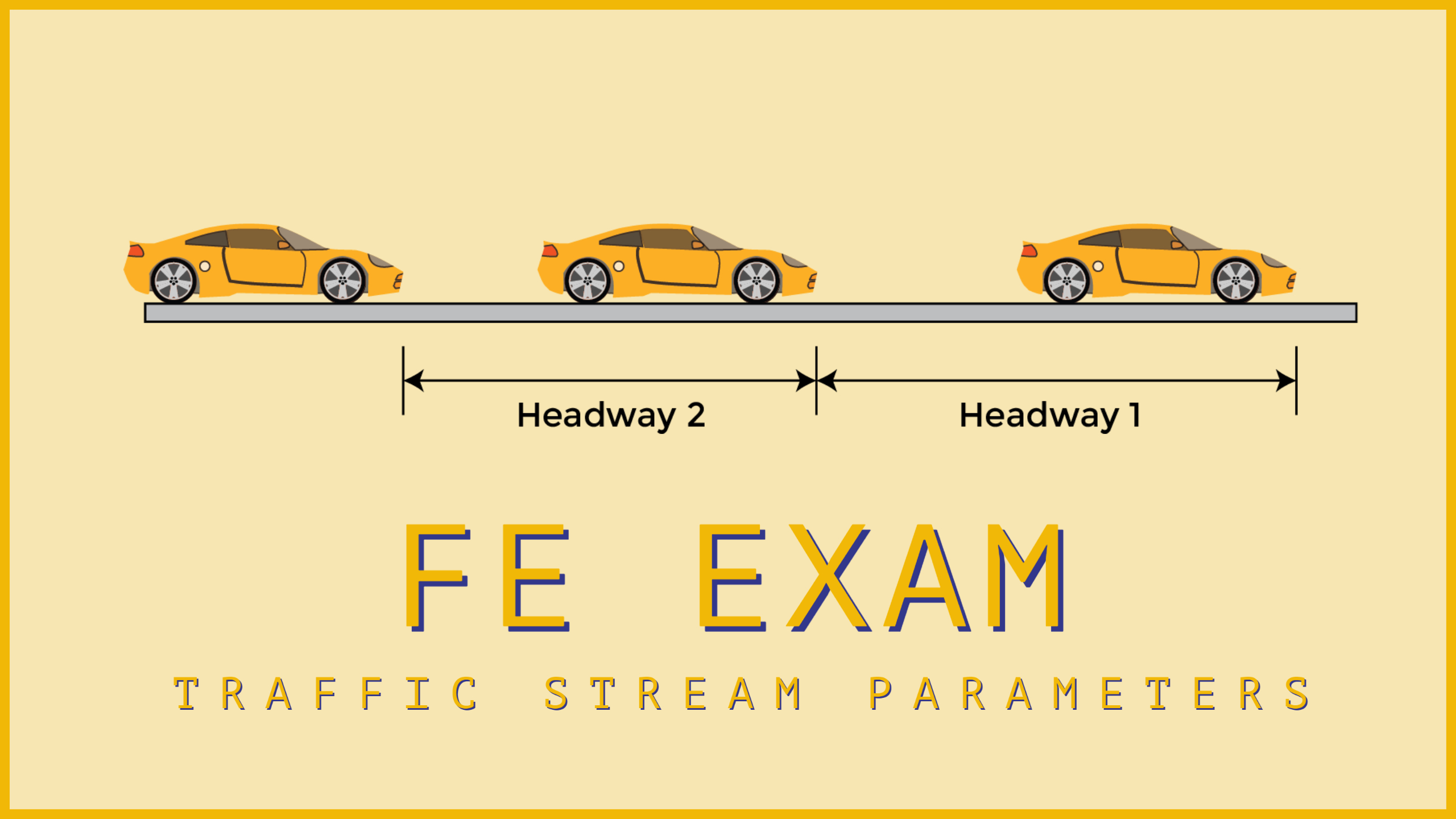
Headway Parameters

Headway (h)

The time (seconds) between successive vehicles in a traffic lane as they pass a point is the headway time. 

The duration of time travel (t) is given by the following equation: 

\begin{equation}
t=\sum_{i=1}^{n} h_{i}
\end{equation}

The flowrate and headway are related through the following equations:

\begin{equation}
V=\frac{n}{t}
\end{equation}

Substituting equations, we will get: 

\begin{equation}
V=\frac{n}{\sum_{i=1}^{n} h_{i}}=\frac{1}{\bar{h}}
\end{equation}

\begin{equation}
h_{(\text {ave })}=1 / V
\end{equation}

Average Spacing (space headway) 

The distance (ft) between successive vehicles in a traffic lane is called the spacing or space headway. 

This will be the spacing is the distance (ft) between successive vehicles in a traffic stream (measured from front bumper to front bumper).

The density and spacing are related through the following equation:

\begin{equation}
D=\frac{n}{L}
\end{equation}

\begin{equation}
L=\sum_{i=1}^{n} s_{i}
\end{equation}

We can combine the top equations and get: 

\begin{equation}
\begin{gathered}
D=\frac{n}{\sum_{i=1}^{n} s_{i}} \\
D=\frac{1}{\bar{s}}
\end{gathered}
\end{equation}

Therefore: 

\begin{equation}
D=1 / s
\end{equation}

Our in-depth Civil FE review course covers everything you need to know about traffic flow. We cover plenty of examples and will show you the step-by-step process that can be applied to analyze traffic stream by considering the flow, speed, density and head properties.